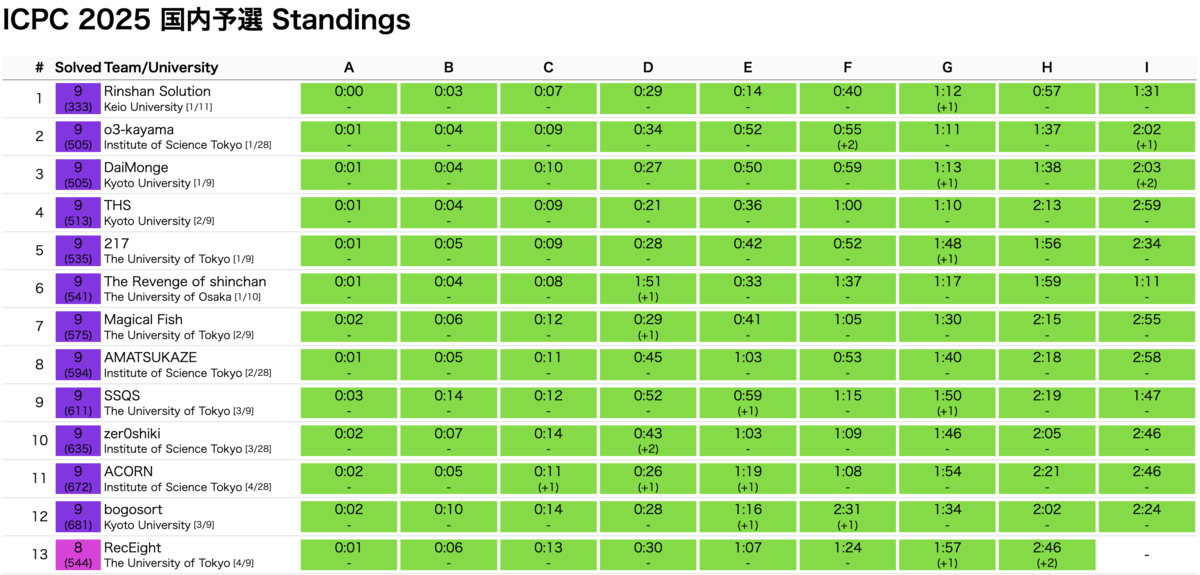
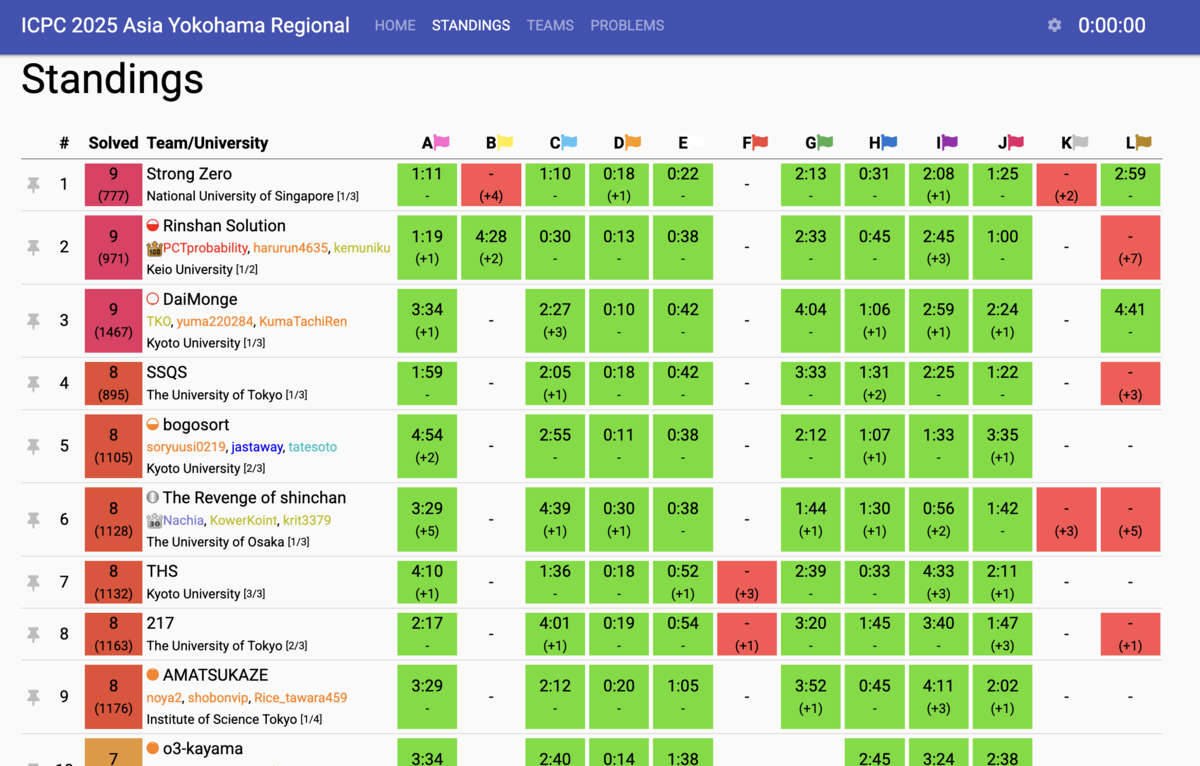
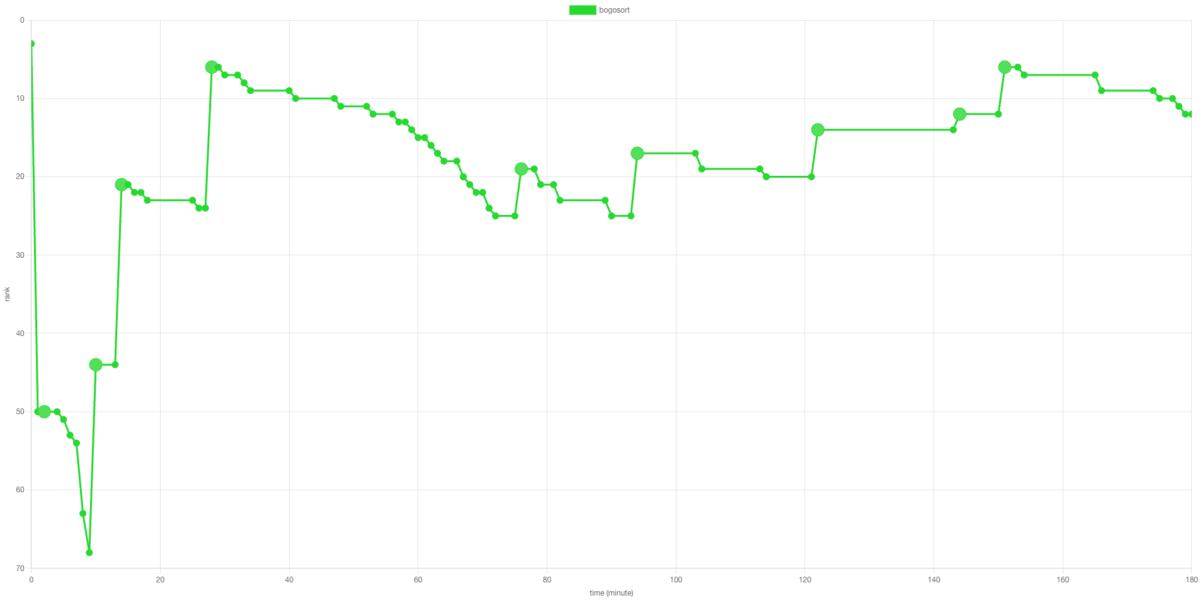
今週の参加記担当の山田です!
ABC437
クリスマスが近づいています。競プロ界隈でクリスマスといえばhosさんの恒例コンテストですが、ABC437もクリスマスのサブタイトルが付いています。ちなみに12/24はSASUKEが見たいのでXmas Contestの方には泣く泣く不参加です。
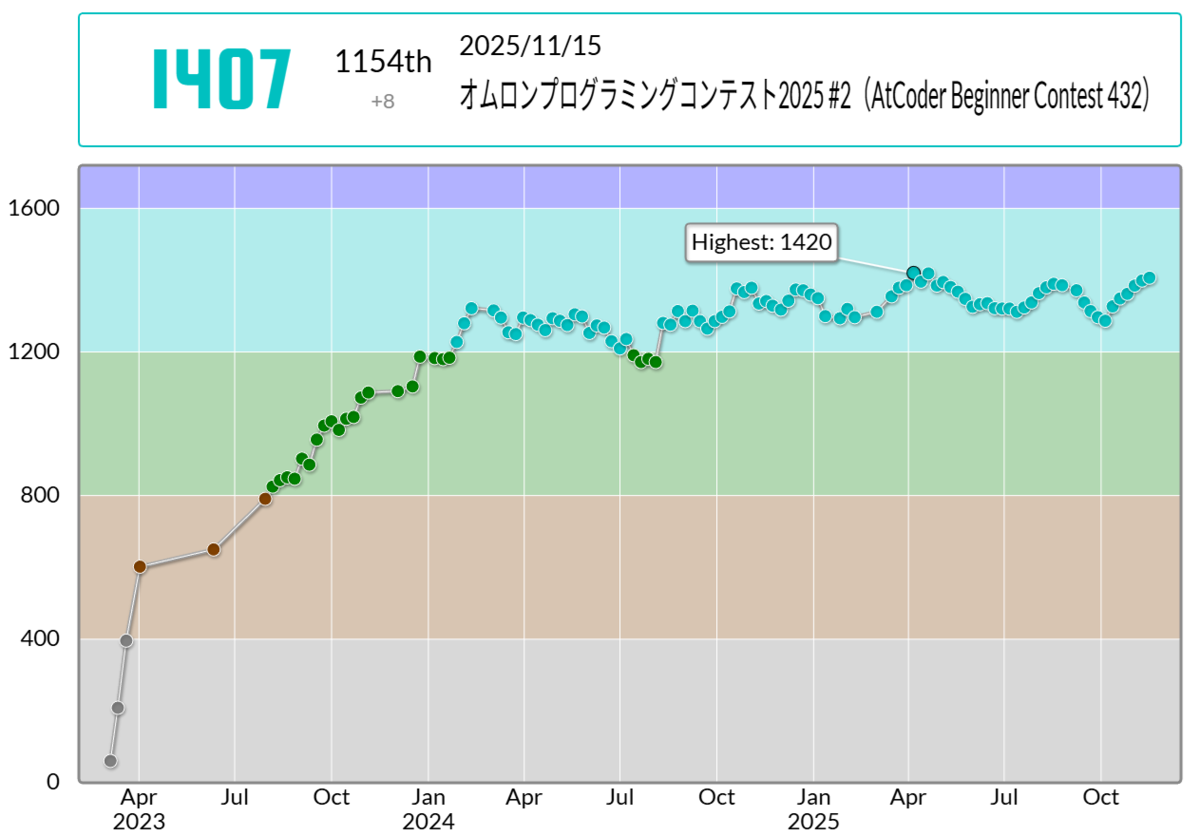
コンテスト開始時点での山田のレーティングは2020だったので今回もRated対象外での参加記となります。
黄タッチ後の山田 vs ABCの歴史を振り返ってみると、カンスト2回、黄perf3回、青perf2回、水perf1回。まだ黄色安定とはそこまで言えないので黄perfが欲しいです。
爆速6完必須回になる確率が高い配点の上、3人全員が警戒しているWriterなので怖いです。
A問題
問題文: A - Feet
difficulty: 43?
KCPCメンバー(Rated参加)のAC率: 14/14
print(A*12 + B)。0:30 AC。
AtCoderの提出の折り畳み使用が変わりました(長すぎると『拡げる』を押しても完全には開かない)。山田を含む、テンプレ激長族のコードが見にくいです。
B問題
問題文: B - Tombola
difficulty: 112?
KCPCメンバー(Rated参加)のAC率: 14/14
コンテスト後に問題名の元ネタを調べたら、イタリアの年末パーティでよく行われる運ゲーらしいです。

要素が相異なるという制約がなかったらちょっと気を付けることが増えます。この問題は何も考えなくても合わせられました。
1:40 AC。
C問題
問題文: C - Reindeer and Sleigh 2
difficulty: 643?
KCPCメンバー(Rated参加)のAC率: 14/14
350点です。難しいC問題に付けられる配点です。C問題だから大丈夫だろうと言いたいところですが、ABC432Cに30分かかる大事件が最近起こったので気を引き締めます。
サンタとトナカイを選ぶ問題かと思いきや、あろうことか登場人物が全部トナカイです。
そっか……トナカイってソリに乗らないんだね(何も考えずに問題文書いてた)
— とりゐ(競プロ) (@torii_kyopro) 2025年12月21日
そして案の定パッとわかりません。
トナカイを一頭ずつ追加していくことを想像してみると以下のDPが有効そうです。
ですがこれだと到底間に合わないです。
dpの形跡から答えを抽出するパートを想像すると、と
の差が非負であればいいので、無駄な情報が相当に多いです。よって以下のようにします。
一次元減らせましたがまだだめです。
ここまでの考察は一瞬で、ここから躓きました。どうやっても高速化不可能です。こういう『値をスライドしてchmax』みたいなDPを高速化する方法は知りません。あったとしても横幅が広すぎて厳しそうです。
DP方針は捨てた方がいいとすぐ判断しました。
というこの問題を表す式でいろいろできないかしばらく考えてみました。しかし変形の余地はありません。
改めて問題設定を考え直してみます(詰まった時は設定の考え直しが有効になりがち)。これは『ソリに乗るトナカイ』という部分集合と『ソリを引くトナカイ』という部分集合を選ぶ問題です。二つの部分集合は競プロ方言でいわゆる分割型です。つまり各要素がちょうど1つの部分集合に属するという形です。
よって選ぶ部分集合は1つで済みます(「全員『ソリを引く』状態がデフォルト。『ソリに乗る』状態にする部分集合を選んでいく」ということになります)。選ばれる要素ごとにの差分が固定されているので、それが小さい順に貪欲でソリに乗せていけばよい、ということがやっと分かりました。難しくないですか!?
実装開始。
と
は、それを合体した
std::pairの配列で受け取ります。std::sortにラムダ式を投げるテクでソートします。(C++erで知らない方は調べてみることをおすすめします)
差分の計算が思ったよりもミスりやすく、サンプルを合わせるのに苦労しました。算数弱者。
10:56 AC。まあ遅すぎではない!
初心者も少なくないKCPCの正答率が100%なのは凄いと思います。本当になんで……?
D問題
difficulty: 664?
KCPCメンバー(Rated参加)のAC率: 13/14
とりあえずの要素を固定してみて
として、答えへの寄与を考えます。つまり
という式で表される値です。これを以内ぐらいで求めたいです。
求める式のシグマの中身に絶対値やmaxやmodみたいな記号はあったら邪魔です。逆にこれを場合分けなどによって消せればすぐ解けがちです。そういう問題は大量に見覚えがあります。
絶対値はと
の大小関係で場合分けすれば外せます。
はあらかじめソートしておきます。
以上になる瞬間の
の添字(
std::lower_boundで求める)をとすると、
これならの累積和を使って定数時間で求まります。これを全ての
に渡ってやります。
13:16 AC。今日の癒し枠でした。
E問題
問題文: E - Sort Arrays
difficulty: 1348?
KCPCメンバー(Rated参加)のAC率: 9/14
根付き木に見立てたくなる設定です。
そもそも木の入力の与えられ方は、
制約
1 ≤ u_i, v_i ≤ N
入力
u_1 v_1
u_2 v_2
...
u_{N-1} v_{N-1}
というものの他に、
制約 1 ≤ p_i < i 入力 p_2 p_3 ... p_N
という風に『親頂点』で与えられるものがあり、この問題のの与えられ方と一致しています。
そうしての値によって構築した木は、まさにTrieと酷似しています。
ですが完全に一致しているわけではありません。Trieは同じ列であれば同じ頂点に所属する、という性質がありますが、入力からそのまま作った木だと同じ数列があっちこっちに発生します。
最終的に辞書順に並べることを考えるとTrieでできます。よって構築すべきはTrieの方だろうと考えました。考察はこれで終わりです。
Trieライブラリは手元にありますが、そのままは使えません。いつもそういう場合はコピペ後に実装を書き足して使用するという戦略を取っています。ですが今回はほとんど0から書き直さないとならなそうです。Trieは自分で作った方がよさそうです。嫌だ……。
実装前に、実装方針を考察用紙に書き出します(最近、実装が重そうなときはこれを徹底しています。実装崩壊率は体感減っています)。
構築すべきものは、
vector<map<ll, int>> g(頂点番号を入れると、遷移先を表す連想配列が返ってくる)vector<vector<int>> lis(頂点番号を入れると、そこに所属する数列番号の一覧が返ってくる)
です。(これ一緒の構造体にした方が分かりやすかったかな……)
これだけ持っておけば大丈夫だろうかと考えてみると、大丈夫じゃないです。『「親の数列」が所属する頂点』が高速に知りたくなるので、
vector<int> pos(数列番号を入れると、それの所属先である頂点番号が返ってくる)
という配列も必要です。以上の3つの変数を同時に動かしながら構築していく必要があります。『同時に動かす変数』の数が多いと指数関数的に実装が大変になるのですが、3つならなんとかなりそうです。
と、思っていましたが配列のサイズも動くので配列外参照が発生したりして、サンプルを合わせるのに時間がかかりました。あと添字が2種類あるので混同して大変でした。
32:27 RE。RE!?
WAもありました。なんでだ。睨みデバッグでは原因がすぐ分からなかったので、必殺・ランダムチェッカーを発動させました。
山田は以下の2種類のシェルスクリプトを使っています。(コンテスト中のものとは少し違います。このブログに載せるついでにGPTと一緒に修正しました)
a.sh
#!/bin/bash g++ -std=gnu++20 -O2 a.cpp -o a.out || { echo "a.cpp コンパイル失敗"; return 1; } echo "a.cpp コンパイル成功" g++ -std=gnu++20 -O2 n.cpp -o n.out || { echo "n.cpp コンパイル失敗"; return 1; } echo "n.cpp コンパイル成功" g++ -std=gnu++20 -O2 r.cpp -o r.out || { echo "r.cpp コンパイル失敗"; return 1; } echo "r.cpp コンパイル成功" cnt=0 while true; do ./r.out > inp ans1=$(./a.out < inp) ans2=$(./n.out < inp) cnt=$((cnt+1)) if [ "$ans1" != "$ans2" ]; then echo "Wrong Answer on case $cnt" echo "===== input (inp) =====" lines=$(wc -l < inp) if [ "$lines" -le 20 ]; then cat inp else head -n 20 inp echo "..." fi echo "=======================" echo "a.out:" echo "$ans1" echo "n.out:" echo "$ans2" break else echo "Case $cnt OK" fi done
r.sh
#!/bin/bash g++ -std=gnu++20 -O2 a.cpp -o a.out || { echo "a.cpp コンパイル失敗"; return 1; } echo "a.cpp コンパイル成功" g++ -std=gnu++20 -O2 r.cpp -o r.out || { echo "r.cpp コンパイル失敗"; return 1; } echo "r.cpp コンパイル成功" cnt=0 while true; do ./r.out > inp ./a.out < inp > /dev/null 2>&1 if [ $? -ne 0 ]; then echo "Runtime Error on case $cnt" echo "===== input (inp) =====" lines=$(wc -l < inp) if [ "$lines" -le 20 ]; then cat inp else head -n 20 inp echo "..." fi echo "=======================" break fi cnt=$((cnt+1)) echo "Case $cnt OK" done
前者a.shは、提出用コードa.cppと、愚直解n.cppに、ランダムテスト生成コードr.cppで入力しまくって、出力が不一致となる入力を見つけるスクリプトです。後者r.shは、提出用コードa.cppに、ランダムテスト生成コードr.cppを入れまくってREの起こる入力を見つけるスクリプトです。
今回はREの起こる入力が知りたいので、使うのは後者のr.shです。これなら愚直解を書かなくて済みます(なのでREで落ちるときのランダムチェックは楽です)。このファイルをカレントディレクトリに置き、r.cppにテストケース生成コードを書き、. r.shで実行、強制終了させたいときは<C-c>(vim方言でCtrl+cのこと)を押します。
無事落ちるケースが発見できました。inpというファイルに落ちた入力が保存されているのでそれを見たり./a.out < inpでプリントデバッグしていきます。すると一か所、 さっきの提出コード上に頂点番号と数列番号を混同している処理を見つけました。サンプルで落としてください……。
38:24 AC。
25分+1ペナ。かかりすぎ! 添字筋が弱い。
F問題
問題文: F - Manhattan Christmas Tree 2
difficulty: 1390?
KCPCメンバー(Rated参加)のAC率: 10/14
マンハッタン距離は45度回転が叫ばれる世の中ですが、何でもかんでもマンハッタン距離を真っ先に回転させるのは良くないと考えています。回転後の座標でばかり考えて沼ったことが複数回あります。そもそも45度回転ってそんなに見かけないです。FFTとかより全然使いません。
そういうことでしばらく元の問題の状況を観察してみました。……しかし『二次元座標の集合に添字の区間クエリを施す』という独特すぎる要求の扱いがわかりません。x座標y座標の値の絡み方がいやらしいです。
45度回転する嬉しさのひとつは1次元の独立な問題に分解できがちことです。結局この問題は積極的に45度回転させた方が良さそうです。
回転後の点からの各チェビシェフ距離(つまり回転前のマンハッタン距離に同じ)を考えると、クエリ2の答えの候補は4方向に最も遠い点の4つに絞られます。これは(x座標, y座標)×(のmin, のmax)をそれぞれ取得できるセグ木(つまり4種類)を管理して更新クエリにも対応できます。(今考えると、マンハッタン距離の等距離線はひし形になるので、唐突に45度回転を持ち出さなくても、『斜め4方向に一番遠い点になるだろう』という予測は可能だった気がします)あと答えは最終的にマイナスにならないので、『上方向の点が存在しない場合』とかは考えなくてOKです。
簡単だこれ!早く実装しないと!!
山田はセグ木を生やす際、いちいちopなどの関数を作るのではなく、ベタな遅延セグ木を1秒で持ち出せるようにしています(ライブラリとかエディタを駆使します)。(区間更新、区間加算)×(区間和取得、区間min取得、区間max取得)の6種類は一瞬で出てきます。さらに同時使用してもテンプレート引数名は衝突しません。まさに山田の競技環境が役に立つ問題です。今回は遅延評価は必要ないですがこれを利用します。
47:38 AC。とりあえず大崖のふもとまで到達。
恐る恐る順位表を開くとギリギリ黄色perf!良かった。でもペナルティで下がりまくりそう。
そしてG問題のACメンツがカラフルです。人間と思われるユーザーにほとんど解かれていませんでした。
G問題(読んだだけ)
問題文: G - Colorful Christmas Tree
difficulty: 2754?
KCPCメンバー(Rated参加)のAC率: 0/14
解けそうにないですけど読んでみました。一見木DPでできそうに見えます。でも根方向から切断していく状況に対応できません。
わかりません。Unratedなこともあり虚無な時間が流れて嫌だったので途中からは撤退しました。
再難所は復元パートらしいですが、そもそも求値のフローにすら辿り着けず……。難しいという先入観がなければ求値はできた可能性はあります。
Upsolveしたら何か追記するかも。
コンテスト結果
47分38秒+1ペナの6完。パフォーマンスは2042相当です。C問題で小炎上、E問題で大炎上して今日はダメかと思っていましたが、DとFが速かったらしく普通の結果となりました。
ABCならちょっと失敗したくらいでは黄perfラインまで下がらないぐらいにはなっており成長を感じます。
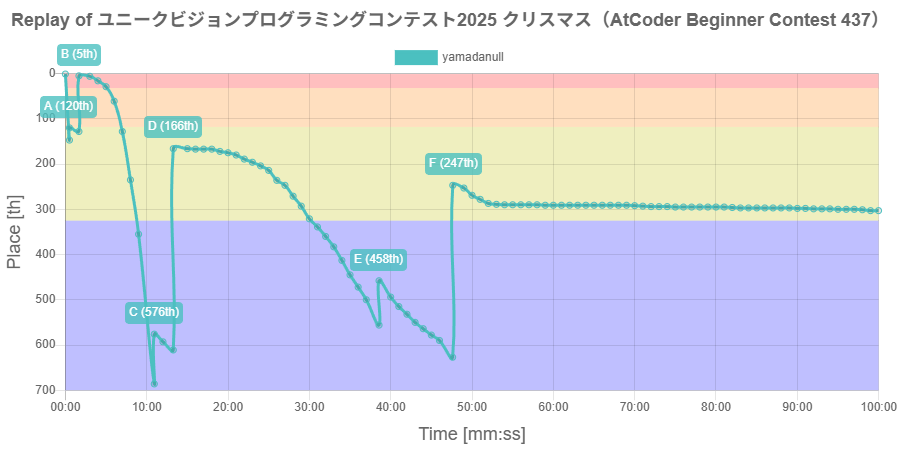
わかりやすくCとEに時間かかってます。DFを先に解いた人が多いのもありますが。こういう問題しか出題されないコンテストがあったら詰むのでそれが怖いです。
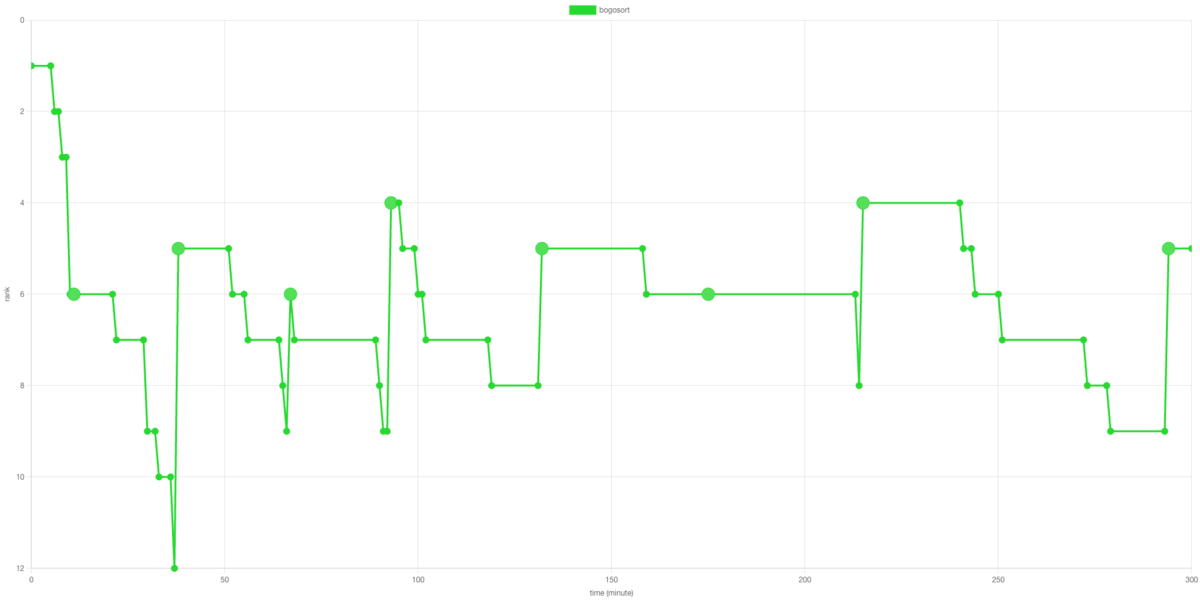
↓画面録画