こんにちは、みうね です!これは AtCoder Beginner Contest 435 の参加記です。
ABC435
9/21のARC206 (Div. 2) で青落ちしてから3ヶ月間くらい1900台で絶賛停滞中です。
先週の ARC211(Div. 2) では2471 perfを叩き出せてレーティング1989まで戻ってきたので、この調子で再入黄をはたしたい!
A問題
問題リンク: A - Triangular Number
推定diff: 48
KCPCメンバー(rated)の正答率: 12/12
コンテスト開始後問題ページを最速で開くには事前にA問題のURLを直打ちしておいて再読み込みしまくればいいというのを今回初めて実践しようと思いました。しかし、それを思い立ったのがコンテスト開始一分前だったためURLの書き換えが不十分で
https://atcoder.jp/contests/abc435/tasks/abc434_a にアクセスしてしまっていました。
普段やってないことをやるときは前もってちゃんと準備しとかないとダメですね〜
問題自体は簡単で、
$1 + 2 + \cdots + N = N \times (N + 1) \div 2$
を覚えてたらOKです。
0:43 AC
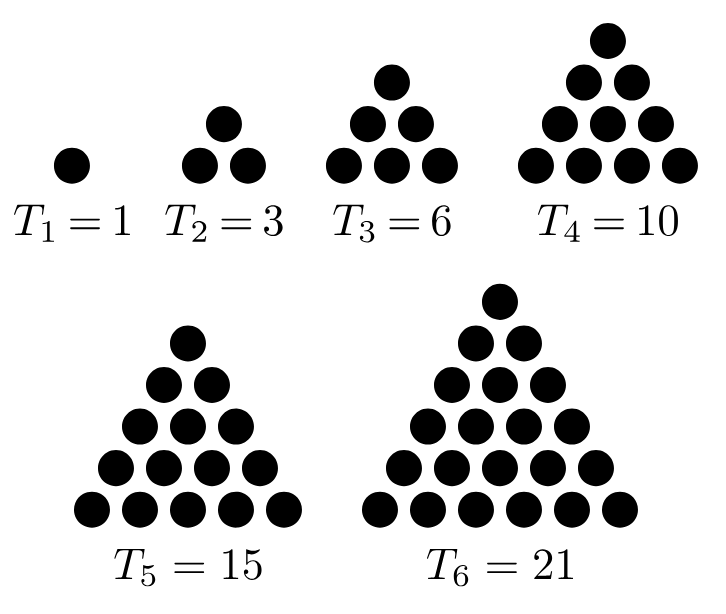
問題名の由来が気になって調べたところ、 $1 + 2 + \cdots + N$ の形で表せる数のことを triangular number と呼ぶらしいです。理由は以下の図のように三角形状に配置できるからだそうです。初知り。
B問題
問題リンク: B - No-Divisible Range
推定diff: 167
KCPCメンバー(rated)の正答率: 12/12 $l = 1 \ldots N, r = l \ldots N, i = l \ldots r$ の三重ループを回せばよいです。これって $N$ が大きくても高速に計算できるのでしょうか。
3:37 AC
C問題
問題リンク: C - Domino
推定diff: 319
KCPCメンバー(rated)の正答率: 12/12
絶対全部倒れない?って思ったけど、 $i + A_i$ 『未満』なので、 $A_i = 1$ のときその右のドミノが倒れないことがあります。
左から順にどんどん倒れていくので、「倒れてるゾーン」の最右の座標を左から順にドミノを見て更新していけば良いです。
5:48 AC
D問題
問題リンク: D - Reachability Query 2
推定diff: 786
KCPCメンバー(rated)の正答率: 11/12
無向グラフなら Disjoint Set Union (Union-Find) で解けますが、今回は有向グラフです。
今回の問題で注意した点は以下の2つです。
一度黒くなった頂点が白くなることは無い
「辺を辿って黒色の頂点に到達可能な頂点」に辺を辿って到達可能であれば、その頂点も「辺を辿って黒色の頂点に到達可能な頂点」である。
この2つの性質から、「辺を辿って黒色の頂点に到達可能な頂点」は黒い頂点と同一視してよいことがわかりました。
よって、辺を逆向きに張ってクエリ1がくるたびにDFSなどを使ってそこから到達可能な頂点をすべて黒色に塗れば良さそうです。DFSをする際、一度黒く塗った頂点に再度訪れる必要はないので、全体の計算量が $O(N+M+Q)$ になることも確かめられました。
10:38 AC
E問題
問題リンク: E - Cover query
推定diff: 1129
KCPCメンバー(rated)の正答率: 10/12
明らかに「区間をsetで管理するテク」で解けそう。
「区間をsetで管理するテク」は確かけんちょんさんが「Interval Set」という名称でライブラリを作ってたよな…と思って検索タイム開始です。
すぐにそれっぽい記事が見つかりました。
「区間をsetで管理するやつ」を「IntervalSet」と呼びませんか #競技プログラミング - Qiita
しかし、肝心のけんちょんさんの IntervalSet のライブラリへのリンクが切れています…(現在は直っています)
けんちょんさんがライブラリの名称を変更していたことが原因だったのですが、私はらいぶらりが一時的に消えてしまっているものだと思ってしまいけんちょんさんのライブラリをパクることを断念して、自力実装をしようという方針につきすすんでしまいました。
区間をsetで管理するテク、やってることはsetの二分探索を使って区間の情報を追加したり消したりするのを対数時間でやろう!ってだけなのでそんなに難しくないと思っていたのですが、実装はやってみると落とし穴がいくつもありました。
とくに2つ目の落とし穴が深刻で、20分以上かけて頑張って書き終えたと思ったら iterator is read-only って言われて全て書き直しになってしまいました。
D問題を通した時は130位くらいだったのに、もう水perf圏内まで順位が落ちてしまっています。自力実装を続けるなら iterator is read-only って言われないように気をつけながらほぼ全てを書き直さねければなりません。
さすがにそんなことをやっていたら日が暮れてしまう…
けんちょんさんのほかにも区間をsetで管理するテクのライブラリを書いている人がいるはず!って思ってもういちどGoogle検索してみると、 std::setで区間を管理する奴 - かっつのメモ帳 という記事がみつかりました。
記事に書かれていたのは私が欲しかったものそのものです。この記事で紹介されているコードに少しの変更を加えるだけでACできそうです。
ということで、時間がかかりましたがひとまず
49:54 AC。
「区間をsetで管理するテク」の自力実装はまた今度ちゃんとやります…
なお、山田くんがセグ木のユーザ解説を書いていましたが、確かに(特にライブラリを持っていない場合は)座圧+セグ木のほうがよい方針だったと思います。
公式解説のような解法は『区間をsetで管理するテク』と呼ばれ、(ライブラリなしであれば)実装の重さに定評があります。
ここ笑っちゃった
F問題
問題リンク: F - Cat exercise
推定diff: 1461
KCPCメンバー(rated)の正答率: 5/12
猫があるタワーに訪れた後、次に猫が移動する際にそのタワーは破壊されてしまうので、その後猫の移動先となるタワーはそのタワーの左か右のどちらかだけに存在します。また、猫があるタワーに訪れたとき、そのタワーから到達可能な範囲にはいま猫がいるタワーよりも低いタワーしかないです。
したがって、猫があるタワーに訪れたあとに右にいけばいいか左に行けばいいかはそのタワーより低いタワーよりひくいタワーのみを集めた連続区間それぞれについて猫の移動距離、それぞれの連続区間の中で最も高いタワーの位置がもとまってたらわかります。
よって低いビルから順番に見て行って、dsuを用いて代表元を管理しつつそれぞれの区間について猫の移動距離と最も高いタワーの位置を管理していけば良いです。
70:15 AC
値の小さい順から見ていくのはわりとよく見るDPなのでこれに550点ついてるのは結構非自明。解説では Cartesian Tree を構築してるけど、その解き方してる人あんまいないんじゃないかなぁ…
G問題
問題リンク: G - Domino Arrangement
推定diff: 2499
KCPCメンバー(rated)の正答率: 1/12
区間制約がない時はDPで解けることが分かったけど…
遅延セグ木でなんとか更新頑張るのかなぁとか考えてたけど普通に線形で解けるらしいです。いやぁ〜むずい
結果

ABCDE5完70:15 で、1727 perfでした。E問題でかなり詰まってしまったのがかなり痛くて、それがなければ再入黄も全然できてそうだったので結構悔しいです。区間をsetで管理するテクはよく聞くテクだったしお気持ちはまあ理解してたけど、ライブラリを持っておらず実装したこともなかったのが今回はかなり痛手になってしまいました。実装力に自信がない人はライブラリをちゃんと整備しよう