はじめに
こんにちは!jastawayです。ABC415の参加記です!!
先日のICPC国内予選では、チームbogosortとして参加し、全完12位で無事通過することができました!
チームメイトに頼りきりになっているので、横浜では自分も貢献し台湾に行きたいと思っています。
そのためにも(?)早く黄色に戻らねば・・・
目次
ABC415
参加前の私のレートは1944でした。
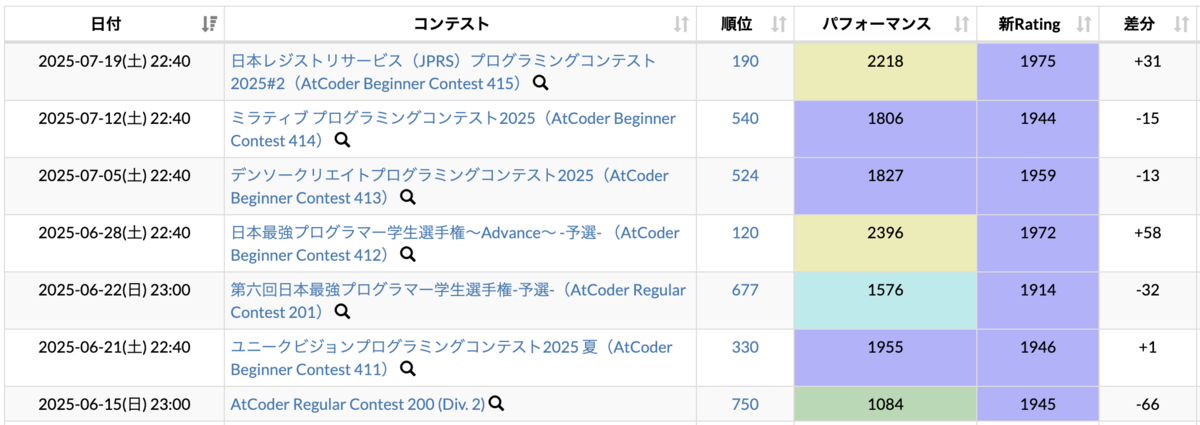
最近の成績は、ARCで負けてABCは耐えている感じで、手順前後で再入黄できてそうな感じもあり、競プロが下手です()
今回の配点は100-200-350-400-450-525-575で全完可能そうです。
カンストパフォでもギリギリ再入黄できなさそうですが、なるべく黄色に近づけておきたいところ。
以下、各問題の考察&感想です。
A問題
問題文: A - Unsupported Type
KCPCメンバー(rated 参加)のAC数: 15/15
推定diff: 45
for文で $A_{i}$ を順番に見て $X$ と一致していたら Yes を出力してreturn 0すれば大丈夫です。
for文を抜けたらNoを出力します。
0:55に提出、AC。
B問題
問題文: B - Pick Two
KCPCメンバー(rated 参加)のAC数: 15/15
推定diff: 85
前のindexを記録して解くことを考えます。
$bf$ という変数を用意しておいて、$-1$ で初期化しておきます。
$i = 1, \dots , |S|$ について $S_i$が# のとき、 $bf = -1$ なら $bf = i$ と書き換えます。
$bf \neq -1$ なら $bf, i$ を出力して $bf = -1$ と書き換えることで解くことができます。
出力形式がいつもと違っていて少し驚きましたが、これはジャッジが空白と改行を区別しないため、# の位置を順に出力しただけで通ってしまうのを防ぐためでしょうか?
3:24に提出、AC。
C問題
問題文: C - Mixture
KCPCメンバー(rated 参加)のAC数: 14/15
推定diff: 786
350点C問題です。
ある薬品の部分集合に対して、その集合に入っていない薬品を追加したときに安全ならばそこに辺を張るというように、部分集合を頂点としたグラフを考えると、これは、空集合 $\emptyset$ から $\lbrace 1, \dots, N \rbrace$ まで到達できるかという問題に言い換えれます。
部分集合をbitで表すと簡単に表現できるので、BFSによって到達可能かどうかを判定することで $O(N 2^N)$ で計算することができました。
C問題にしては難しいです。さすが350点。
8:19に提出、AC。
D問題
KCPCメンバー(rated 参加)のAC数: 15/15
推定diff: 966
コーラの中身が入っているかどうかは関係ないので、瓶のみに注目して考えればいいです。
交換 $i$ を使うと、$A_i - B_i$ 本減少するので、基本的には $A_i $ と $B_i $ の差が小さい交換を使うのが最適です。
しかし、この交換は $A_i$ 本以上持っていないと使えないというところに注意が必要です。
そこで、$A, B$ を$A_i - B_i$ の小さい順にsortしておき、前から貪欲に交換をすることを考えます。
交換を1回1回シミュレーションするのは、$N \leq 10^{18}$ の制約から、最悪 $N$ 回計算することになり、間に合いません。
そのため、交換 $i$ が何回できるのかを計算する必要があり、不等式を立てて考えると、 $\left\lfloor \dfrac{N-A_i}{A_i - B_i} \right\rfloor + 1$ 回であることがわかるので、 $N$ と答えを更新しながら1回も交換できないところに注意して書くと通ります。
16:57 に提出、AC。
E問題
問題文: E - Hungry Takahashi
KCPCメンバー(rated 参加)のAC数: 12/15
推定diff: 1290
初期の所持コイン $x$ には単調性があるので、この最小値は二分探索したくなります。
そのため、初期所持コインが $x$ 枚の時に最後までできるかの判定問題を考えます。
$dp_{i,j} =$ 「マス $(i, j)$ にいて、ご飯を買った後の所持枚数の最大値」
というDPを考えると、遷移が2つしかないので、 $O(HW)$ の計算量で判定問題を解くことができます。
あとは二分探索を書いて提出!
23:29 に提出、AC。
F問題
問題文: F - Contraction
KCPCメンバー(rated 参加)のAC数: 5/15
推定diff: 1584
ここまで非常に順調です。Fを早解きしてGに時間を残したいところ。
文字列の1点更新と区間クエリなので、segtreeに乗せたいお気持ちです。
そして、この最大の連続部分というのは、両端の情報を持たせておくとsegtreeのマージができるので、すぐにsegtreeに乗せることを考えました。
はじめ、必要な情報として、各文字の頻度と両端の文字だけあればいいと勘違いして、頑張って実装して提出しましたが WA・・・
両端の文字だけではそれが最大の長さとは限らないので、左右の連続する長さの情報も必要でした。
区間がすべて同じ文字のときにマージが少し変わるので、少し実装で楽をするために、その区間の長さの情報も持たせるようにしました。
各文字の頻度はサイズが26で固定なのでvectorで持つのではなく、arrayで持って少し高速化を図りました。(vectorをsegtreeに乗せるのは結構遅くなると聞きます)
めんどくさい実装でしたがなんとか書いて提出!!!
47:33 に提出、AC。
よく考えると頻度は持つ必要なくて、最大の長さを持つだけで十分でした・・・
G問題
問題文: G - Get Many Cola
KCPCメンバー(rated 参加)のAC数: 1/15
推定diff: 2176
Fで1ペナはあるものの、早解きはできてます!Gを解いて勝ちを確定させたいです!
D問題と設定はほとんど同じで、制約と最大化する目的関数が違います。
Dと同じように $A_i - B_i$ の差が小さいものから貪欲に使えばできそうな気もしますが、そんなことはないです。
制約の $B_i < A_i \leq 300$ というのがヒントそうです。
しばらく考えて、 $N$ が小さい時は
$dp_{i} = $ 「 $i$ 本の空き瓶を持っているときに飲めるコーラの最大本数」
とすると、各遷移が $O(M)$ 回で合計 $O(NM)$ で解けることがわかりました。
また、$A_i, B_i \leq 300$ なので、重複を削除すると、$M \leq 90000$ 程度に減らせることもわかりました。
$N \leq 10^{15}$ なので、このままではダメですが、予想として、ある一定の本数になるまでは、貪欲に使えばいいのでは?というのを考えました。
詳しくは考えていませんが、たまに出てくる典型で、効率が悪い方を $s$ 回使うなら、良い方を $t$ 回使えばいいみたいなやつがあって、$A_i, B_i$ が小さいので、こういうのが使えるだろうと予想しました。
そこで、適当にTLEしない程度の定数 $X = 300$ として上記の貪欲で $N$ が $X$ を下回らない程度に減らしてから、DPをしてみます。
とりあえずサンプルが合ったので提出!!!
どうせWAするだろうな〜と思っていましたが、なぜかどんどん通っていってこれはもしや!?となりましたが、最後のケースでWA😭😭😭
時間に余裕がありそうだったので、 $X$ を増やしながらどんどん提出してみますが、最後のケースがずっとWAです・・・
このケース強すぎるよ〜〜〜
手元で色々なケースを試しているうちに、この貪欲はダメなのでは?と思い始めました。
この評価では, $(2, 1)$ と $(300, 299)$ が同列ですが、前者は1本減らして1本飲めるのに対して、後者は1本減らして299本飲めるので、明らかに後者のほうがいいです。
そこで $\dfrac{B_{i}}{A_i - B_i}$ の大きい順でsortして、貪欲してみました。
$X=1000$ で提出してみますが、WA・・・
時間に余裕が合ったので、おもいきって $X=30000$ として提出してみました。
91:37 に提出、AC。
通ってしまいました!!!
正当性を証明せずに通してしまいましたが、まぁACはACですから(ごめんなさい)
修了後解説を見て、$A_i$ が同じなら $B_i$ が最大のものだけ考えればいいというので、確かに!となりました。これくらいは思いつかねば・・・
上の貪欲にしていいという予想は合ってたので良しとしましょう。
コンテスト結果・感想
全完(91:37 + 6ペナ)で 190位、2218パフォ、レートは1944→1975でした!
ペナは多いですが全完です!!
最近は院試勉強などでコンテスト以外ほとんど競プロができていませんが勝てて良かったです!!
院試が終わればICPC横浜に向けてガッツリやるつもりです!!
ARC div.1も出る予定ですが果たして勝てるのか・・・
生成AIの禁止によって序盤が比較的簡単になるかもなので勝って再入黄したいです!!!