はじめまして!今年の春からKCPCに入りました、京都大学工学部電気電子工学科1回生のはるはるです。
この度、コンテスト後の参加記執筆者に加入しました。どうぞよろしくお願いします!
さて、今回はABC405の参加記です。
ABC405
僕のコンテスト参加前のレートは1395でした。今回が僕の初めてのブログ回ということで、始まる前から意気込んでおりました。4月頭にhighestを更新したのちじわじわ下がってきているので、是非とも勝ちたいところです。 配点は100-200-300-400-475-525-625で、普段E問題が分水嶺となる僕にとっては若干厳しそうな配点です。
A問題
問題文:A - Is it rated?
推定diff: 49
KCPCメンバー(rated参加)のAC数: 14/14
レートRが与えられ、そのレートのユーザーがARCのdiv.Xにrated参加可能か判定する、という問題です。
Xが1か2かで場合分けし、Rが範囲内に収まっているか見るだけです。 大小評価の部分は、pythonだと1600<=R<=2999というような両側から挟む書き方ができて便利です。
01:15にAC。
余談ですが、0完するのが怖くていまだにARCに出たことがありません...。考察重視の問題も練習しないとですね。
B問題
問題文:B - Not All
推定diff: 139
KCPCメンバー(rated参加)のAC数: 14/14
はじめは「各数字について最初に出てくる場所に注目し、それらの中で最も後ろに出てくる数字までを削除する」という解法を書きましたが、サンプル2で落ちたためナイーブな解法を書くことにしました。(今見たら最初のコードをちょっと書き換えることで通りそうですが...)
「渡した数列に1以上M以下の整数がすべて含まれるか」を返す関数を定義し、Aの要素を末尾から1つずつ削ってその関数に渡しました。だいぶ雑ですが制約がゆるいので通ります。
06:49にAC。
C問題
推定diff: 187
KCPCメンバー(rated参加)のAC数: 14/14
二重シグマの問題です。
シグマを展開すると$ A_{1}A_{2}+A_{1}A_{3}+A_{1}A_{4}+...+A_{1}A_{N}+A_{2}A_{3}+A_{2}A_{4}+...+A_{2}A_{N}+...A_{N-1}A_{N}$となり、これは$A_{1},A_{2},...,A_{N}$でくくると $ A_{1}(A_{2}+A_{3}+A_{4}+...+A_{N})+A_{2}(A_{3}+A_{4}+...+A_{N})+...+A_{N-1}(A_{N})$となります。
ある要素から末尾の要素までの和は、累積和を用いて高速に計算できます。 よって、$i=1,2,...,N-1$について、$A_{i}(A_{i+1}+A_{i+2}+...+A_{N})$を求め、それらを足せばよいです。
08:13にAC。
最近はC問題は難しいのがトレンドですが、今回のは比較的簡単でしたね。
D問題
問題文:D - Escape Route
推定diff: 642
KCPCメンバー(rated参加)のAC数: 14/14
グリッド上の(少し変則的な)最短経路探索問題です。 最短経路を見つけることに加え、任意の通路マスからの最短経路の復元(正確には移動方向)も要求されています。
まず各マスからの最短経路を求めるパートですが、愚直に各マスからBFSを行うと計算量が大きくなりすぎてしまい、実行時間超過になってしまいます。
そこで、発想を転換し、ゴール(非常口)を始点としたBFSを行うことで、1度のBFSですべての通路マスの、最も近い非常口からの距離を求めることができます。
この問題では非常口が複数ある場合があり、そのときは探索開始地点を増やします。BFSを行う際のキューにすべての非常口の座標を入れておけばよいです。多始点BFSなどと呼ばれます。
多始点BFSの類題(ネタバレ注意!):
ABCの過去問
JOIの過去問
なお、非常口がない場合は問題文の制約よりすべてのマスが壁マスであるため、入力をそのまま出力します。サンプルになかったらここで詰まってそのままコンテストが終わっていたことでしょう。恐ろしいです...
次に、最短経路に向かう矢印を書き込むパートですが、これは各通路マス$(i,j)$について、そこと隣接する通路マスのうち、非常口までの距離が$(i,j)$より1小さいマスに向かう矢印を書けばよいです。そのようなマスは必ず一つ以上存在するため、矢印に従って移動することを繰り返せば非常口までの距離は必ず1ずつ縮まり、この時の経路は最短経路となるからです。
最初非常口が複数あることに気づかず、1ペナを出してしまいました...。サンプル3で落ちたときにきちんと確認すべきでした。
25:29にAC。
E問題
問題文:E - Fruit Lineup
推定diff: 1337
KCPCメンバー(rated参加)のAC数: 12/14
見るからに数学チックな数え上げの問題です。かなり苦手そうです...
リンゴの位置はすべてのバナナ、ブドウの位置よりも左であるため、まずはブドウとバナナのうち一番左にあるものの場所を考えたいです。
ここで、
・一番左のブドウが、一番左のバナナより左にある場合
・一番左のバナナが、一番左のブドウより左にある場合
という2つの場合分けを考えました。
こうすれば、前者の場合はすべての果物の、後者の場合はバナナ、ブドウ、リンゴの存在し得る範囲を限定できます。
・一つ目の場合分け
はじめは一番左のブドウの位置を全探索しようと思っていましたが、書いてみると実は一番左のブドウの位置は一か所に定まることがわかりました。リンゴとオレンジはすべて一番左のブドウより左になければならず、バナナは仮定より一番左のブドウよりも右に存在するので、一番左のブドウの位置はA+B+1に限定されます。
このとき、リンゴとオレンジの配置は${}_{A+B} C_A$通り、バナナとブドウ(一番左は固定しているため、残りD-1個)の配置は${}_{C+D-1} C_{D-1}$通りとなります。
・二つ目の場合分け
今度は一番左のバナナの位置を全探索します。 一番左のバナナの位置が定まると、一つ目の条件よりリンゴの配置の通り数が定まります。
そして、オレンジとブドウの配置についてですが、これはリンゴとバナナの配置が定まると一意に定まります。すべてのオレンジは一番左のブドウより左にあるので、リンゴとバナナ以外の枠は[オレンジ、オレンジ、オレンジ、...、ブドウ、ブドウ]という風に埋まります。
(ただし、このときの一番左のバナナの位置は、それよりも右側に残りC-1個のバナナとD個のブドウを入れられるような場所である必要があります。)
一番左のバナナの位置を$i$とすると、リンゴの配置の通り数は${}_{i-1} C_A$通り、バナナの配置の通り数は${}_{A+B+C+D-i} C_{C-1}$通りとなります。
あとはこれらを足すだけです。なお、二項係数を998244353で割った余りを愚直に計算しようとすると時間がかかりすぎてしまうため、工夫する必要があります。解説と実装例は外部サイトに丸投げさせてください。
81:23にAC。あと10分解けるのが遅かったら緑パフォで激冷えしていました。
F問題
推定diff: 1621
KCPCメンバー(rated参加)のAC数: 5/14
円周上にあらかじめ弦を張り、クエリでは与えられた弦との交差回数を調べます。 コンテスト時間は全然残っていなかったので、問題を見てタイムアップです...
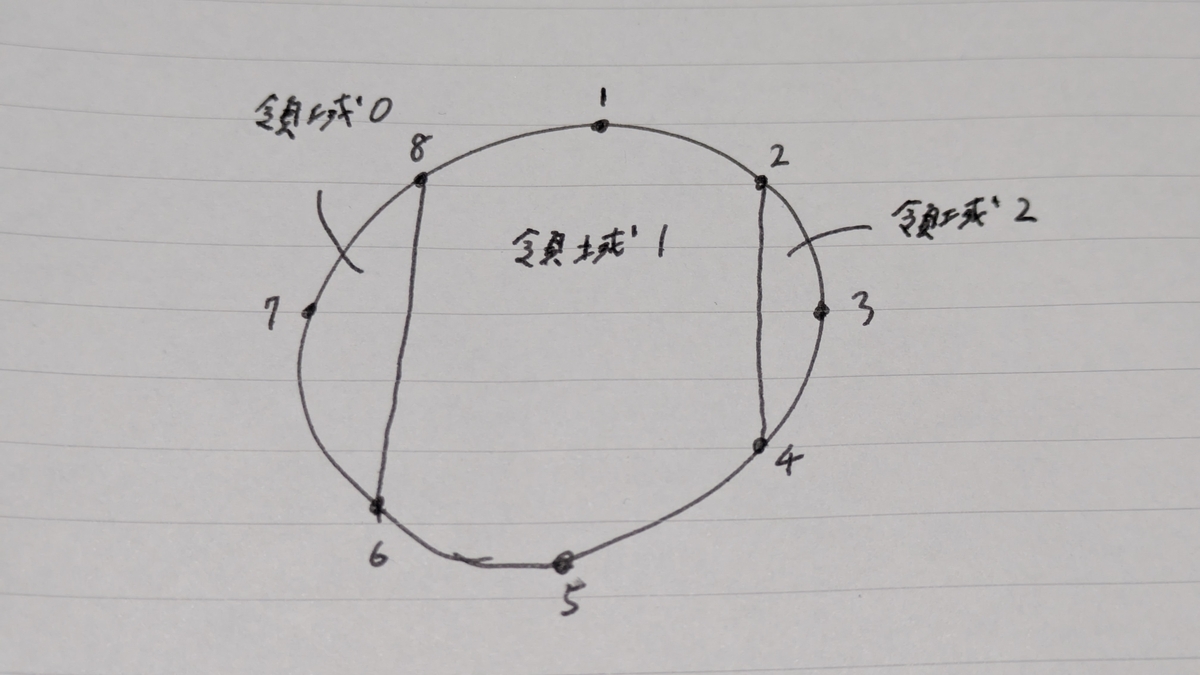
上の図のように、弦で区切られた領域に端から連続する番号を割り振り、クエリでは線分の両端それぞれを含む領域の番号の差の絶対値を答えればいいか?と考えましたが、
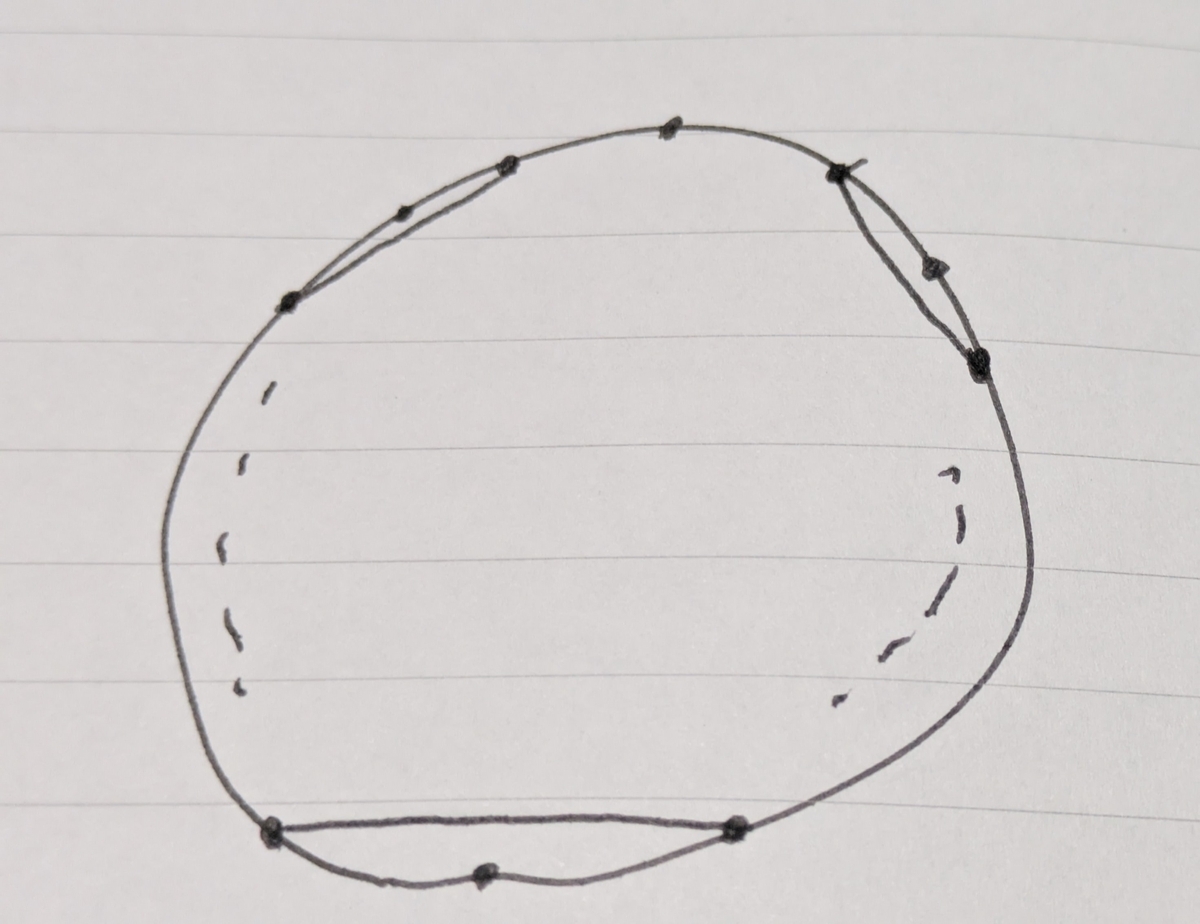 弦がこんな感じのときにバグってしまいますね。
弦がこんな感じのときにバグってしまいますね。
コンテスト後
結果は81+5分でABCDEの5完で、パフォーマンスは1253、レート変化は1395→1381(-14)でした。
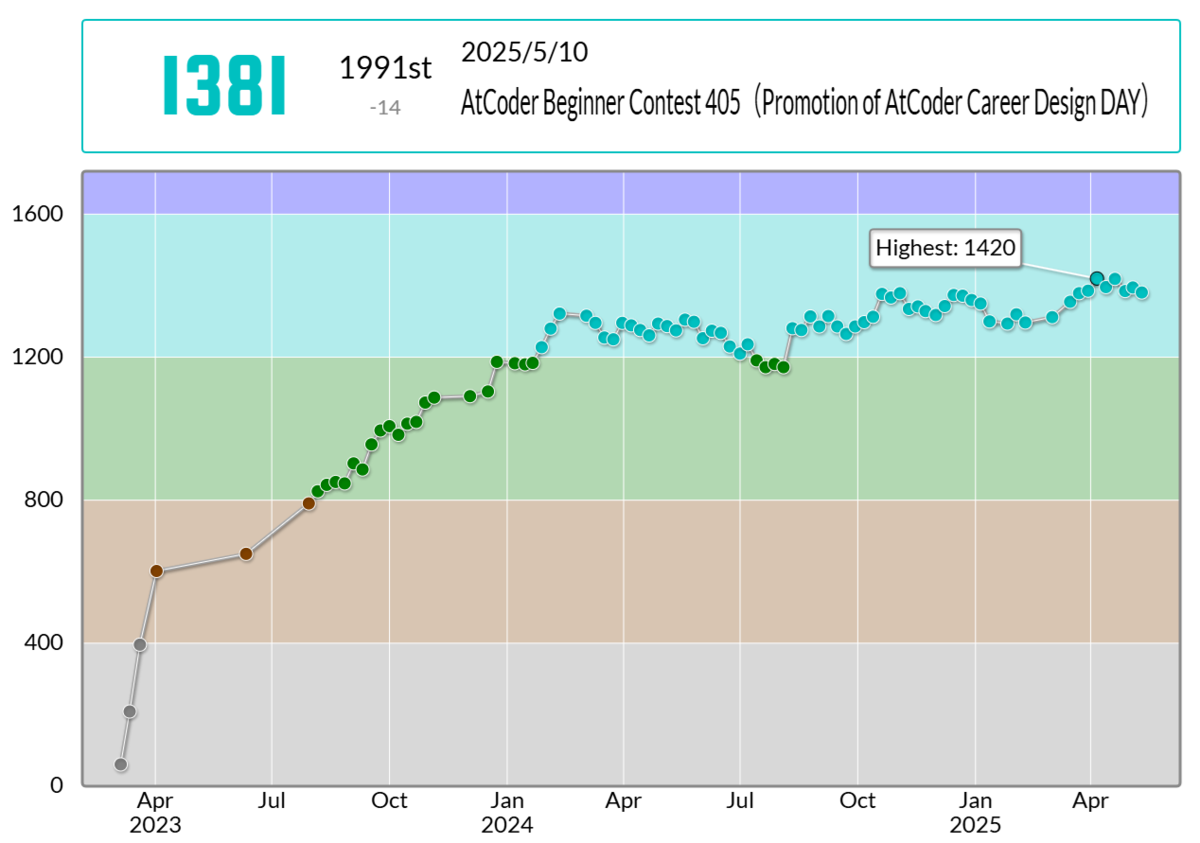
残念ですが、苦手な数学系の問題解けたのでよしとしましょう。 反省点はDの実装でグダってしまった&問題文を読んでいなかったがための1ペナです。
青になるべく、精進を頑張ります!これからもよろしくお願いします。